Write UP - BreizhCTF : Save The World [CRYPTO]

breizhctf

This write Up present the resolution of the Save The World Crypto Challenge proposed during the BreizhCTF 2k18 this Week end.

This challenge has been solved 1 time and was rewarded of 275 points.

Introduction

This Challenge was presented with this message :

L’un de nos agents infiltré en Poldavie nous a envoyé un message suivi d’une trame Pcap, récupérez les codes de désactivation nucléaire afin d’éviter l’apocalypse !

followed by two files :

SOS.txt
bzh.pcap

The SOS.txt file contains the following message :

Je vous annonce que la Poldavie a officielement enclenché le processus d’attaque nucléaire.

Les missiles sont armés et sont programmés à se lancer le samedi 21 Avril 2018 09h AM GMT+2. Le monde entier est visé, tout les pays à l’exception de la Poldavie seront rayé des cartes.

Le seul moyen d’éviter l’apocapypse serait de trouver le code de désactivation nucléaire. Ce code est contenu dans un serveur extrêmement sécurisé et accessible uniquement aux généraux Poldaves. Néanmoins j’ai réussi à y avoir un accès physique et sniffer tout ce qui pouvait y entrer et sortir >pendant quelques minutes.

A première vue, pendant ce temps une vingtaine de généraux ont récupérés ce code sur le serveur : Le serveur récupère la clé publique du général et lui envoi le code chiffré via RSA.

Pour l’instant c’est tout ce que j’ai pu en tirer, envoyez le tout à vos experts en cryptologie et >prions pour qu’ils puissent trouver un moyen de récupérer ce code…

N’oubliez pas, si le code n’est pas retrouvé avant 9h, nous sommes tous perdus…

Bond

We can extract from this message the following interesting informations :

The attached pcap contains the communications between the generals and the secure server
Around 20 generals recovered the wanted secret code
The secret code is ciphered by RSA

Analysis of the pcap file

Now let’s see what does contain the bzh.pcap :

The first reflex we can have is to open it on wireshark and see what does this pcap is looking. In that case, if we analyse a litte bit, we observe some communication between generals and the server. We can determine :

All generals have differents IP addresses
The IP address of the Central server is **192.168.56.105**
The generals and the Central server communicate by simple tcp packets without encryption :
The public keys used to the encryption are plain.

Extracting the TCP streams from the pcap

We know that around 20 generals recover the secret code in this pcap, in order to get all the streams of this pcap in differents files, I propose the following bash script :

#! /bin/bash

mkdir -p output

for stream in `tshark -r bzh.pcap -T fields -e tcp.stream | sort -n | uniq` 
do
	echo $stream
	tshark -r bzh.pcap -w output/general-$stream.cap -2 -R "tcp.stream==$stream"
done

Note : This script must be run from a no-root user

It will extract all the different tcp streams found in the bzh.pcap into the output directory. This is the list of the extracted files :

breizhctf

exactly 20 tcp streams have been extracted, let see now what are they looking like :

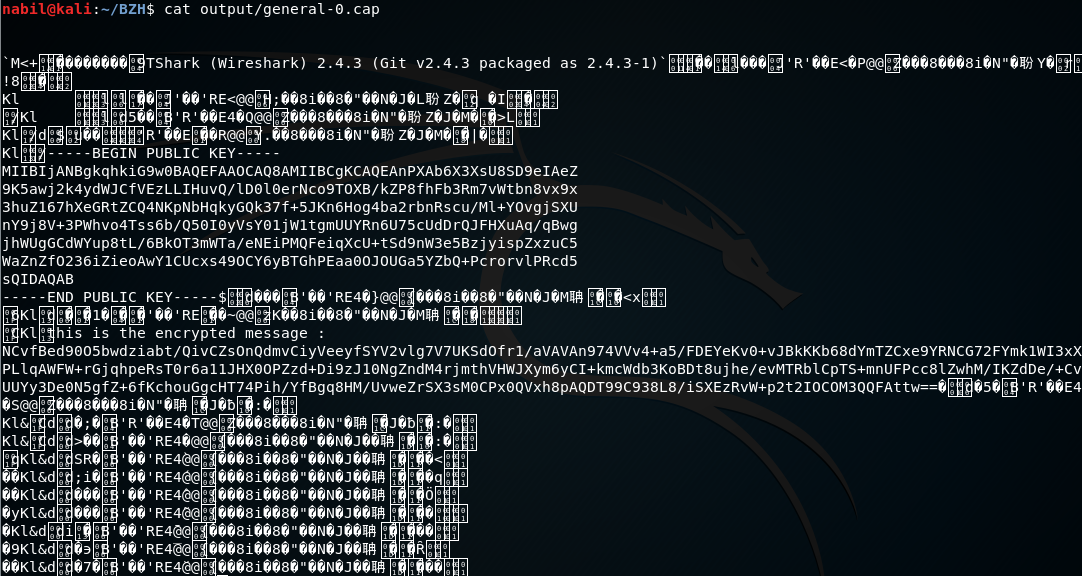
breizhctf

We can clearly recognize the Public Key <-> cipher exchange, both encoded in base64.

Analysis of the RSA public keys

Now, analyze the public keys to determine if they are vulnerable to known attacks :

This is the information from the first public key (general-0.pcap) :

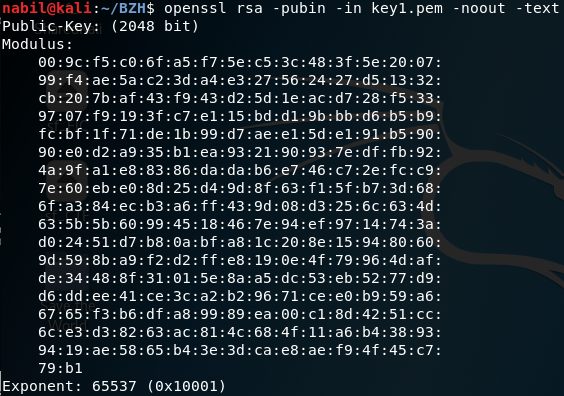
breizhctf

We can see that the key size is 2048 bits, and the public exponent 65537… Nothing show that a possible vulnerability exists. You can run any existing tools to crack this key, but nothing will return. It seems to be a perfect secure public key :/ (for the time being)

But, we have to keep hope and analysing the other keys, because some keys later… we can fiund this key :

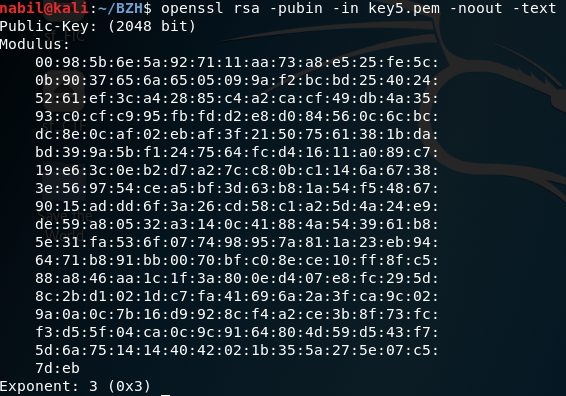
breizhctf

This public key (key5.pem) has been extracted from the general-5.cap stream.
The difference with the other common keys is that the public exponent is 3 !
And if we analyse all the keys, we cand find that 4 other keys have this small exponent !

This is the list of the keys that they have 3 as public exponent :

general-5.cap
general-6.cap
general-12.cap
general-15.cap
general-19.cap

It’s time to see what we can do with this… :)

Attacks against low public exponent : the Coppersmith's / Broadcast attack

A lot of attacks exists against low public exponent, but in our case one is the more suitable : the Coppersmith’s attack. z

First, I will Introduce the technical attacks, from which mathematical properties this attack is possible. And after that I will give an example by cracking the secret code of our chall :)

A little bit of mathematics :)

Some Reminder

RSA
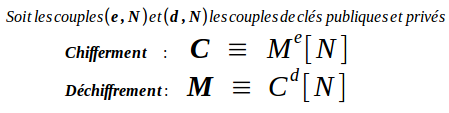
breizhctf

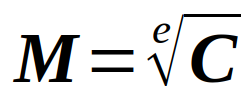
Naively, we can assume that we can revover the cipher from the public exponent this way : tpctf

But it can’t work because :

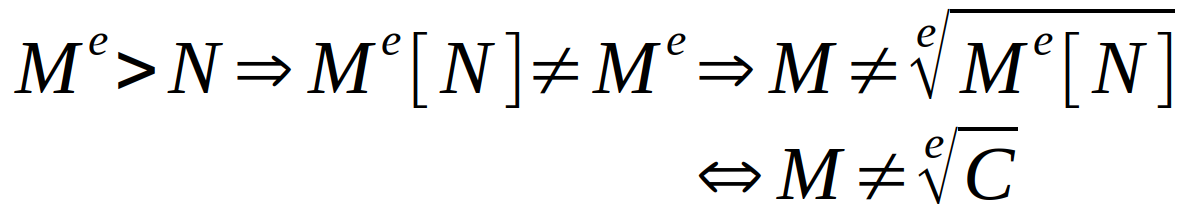
breizhctf

That is why we use padding to ensure that M^e > N

For our attack, we will need a famous cryptographic algorithm :
CRT - Chiness Remainder Theorem

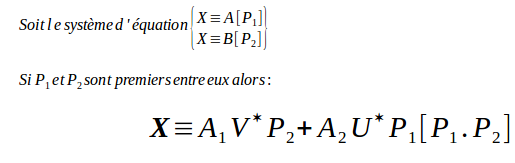
breizhctf

(* U and V come from the Bézout’s identity)

Mathematical Coppersmith's attack

Now we get all the element to perform this :

Let M the plain message
Let (e1,N1), (e2,N2) and (e3,N3), 3 public key pairs such as e1 = e2 = e3 = 3 and N1 ≠ N2 ≠ N3
Let c1, c2, c3 : 3 ciphers respectively encrypted by the 3 public keys
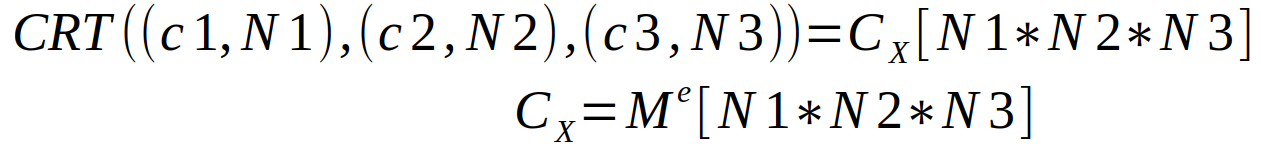
Then : breizhctf

and we can deduce :

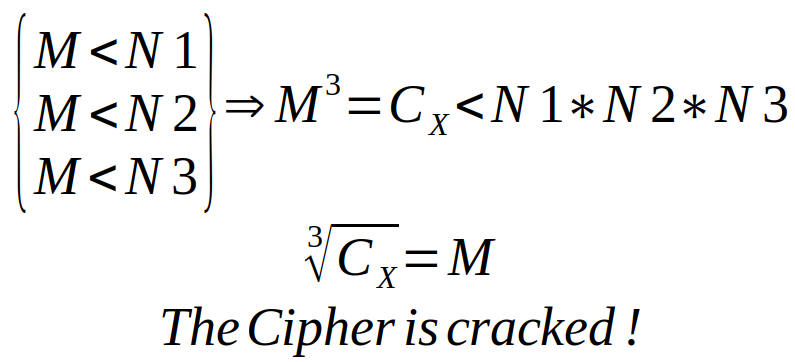
breizhctf

Implementation of the attack

let’s take the steps :

Compute Cx = CRT((c1,N1),(c2,N2),(c3,N3))
Compute M = 3rd root of Cx

I propose the following code (using my cryptographic library)

from CRYPTO.Attacks import broadcast_attack
import binascii
import base64

# Modulus have been extracted from openssl command
# Cipher and modulus of the general 5
c_gen5 = "UxbuEXwHfFI1EAfoMUIdGAVo1qsMMyFRSdZGh9XyUX5VmOBd2b4ZL8aVsuqN3mgceBFcAjbbC+o/cmL3tiBiUTWVlnku6ymBaD6HbpxukHAWsIa/MasXusQw7YhfmzvQSm/a46BJfdxm2fBG2jDU5qJN7I6WWkkREhf6tcRwFn6WLMoFuSV6IqMPSyMZKxGWCLjzWP8mX9v0/kMJjnVY8m98awHnABpZocIBwQTmIpZ89tTaUS/bLIxUskJw+imbAGCSIKDQo5dw/WBDJX/5dEVvS3N+6yfdMBn8beOKrF6yyEy2Vv67R/YwKIKhhOut8L8opfeud1zxX0bY+VEQTA=="
N_gen5 = 0x985b6e5a927111aa73a8e525fe5c0b9037656a6505099af2bcbd2540245261ef3ca42885c4a2cacf49db4a3593c0cfc995fbfdd2e8d084560c6cbcdc8e0caf02ebaf3f21507561381bdabd399a5bf1247564fcd41611a089c719e63c0eb2d7a27cc80bc1146a67383e569754cea5bf3d63b81a54f548679015addd6f3a26cd58c1a25d4a24e9de59a80532a3140c41884a543961b85e31fa536f077498957a811a23eb946471b891bb0070bfc08ece10ff8fc588a846aa1c1f3a800ed407e8fc295d8c2bd1021dc7fa41696a2a3fca9c029a0a0c7b16d9928cf4a2ce3b8f73fcf3d55f04ca0c9c9164804d59d543f75d6a7514144042021b355a275e07c57deb

# Cipher and modulus of the general 6
c_gen6 = "UQ5lLghZvTSzeACqR55+uQjNkZRg3cNWb6NuWNT6gEIYOPh65M+WxBdVR6ecpzy90G6uAMuEgmTelIlgQ2CIgW8FMDyb7ySRu1Bg21kqY68PfbHQVLINtAvPvEIeBm+80MNGLmI0bnXsvI0xkpEicfSIkm9Z27YLYJuI35CKqojoBwExM4QXFamoIVVcCojqRn+9Let5XQaupxGg/AuKd8Smb0z/LlxycOgd3P0+0X3ucBmTe2JiTXx1nKBoKoohl+lxAaoySqSyGMV7Zobo1U0C5W4xYvhfWjganmbvVCLhBmMtzb6EoYY+7yjxdA6KGFwmbQMgb/BQXvaQGpgJYA=="
N_gen6 = 0x7de8abf2d4a082c2a947371aecdb667650938911394a40f69f827f85bd431648aee6cd282b78b4288733321b5f18d81411e4788c9c3c8156b1f1f429b481a58c7c9fdd9737162aecc84e78cf2b1788cf6c0c67b11d0b775314be3e690d20754cdb45b397f5a824cb3cdc183aea0d9642d3c0fa3114f15edadc11886eb34a54fbf4930121012148a76336ba8e3539bcd114318401c3ab0a604a0fe32ad85ab42d368bcd65bf6c67cbdaabdc1ee57c14b487162b549cdc81231cfe04e035f2c65a2de594d912221130e0f4051c121e709c97d45e78c661629b342bb8f10b3a1d4381dbc8e8e23a33decfa37fb2293f16e6d18d9dd8258c1ef19f29b41a5e640fbb

# Cipher and modulus of the general 12
c_gen12 = "NEIe0WtODC7MsN/MvmNLJJHRCyiJUxu8nfHUFOzbl85lsby96ETdoE5YpePeP5Nc2yAULDcWNqg03b345BB5yfGwxs1QnsgHt4fBvWIa3afQOZvzPdQbXMm0Eu51onas25+Y4Nxbp3hW++xvvtcfZwBL2DAmvhfqWTEvDDcWuUVcyDQSygxnCyzKyIYjJES1SzPTPslj6hoN30MnY/Ug97MFWpXQR0v4bNPKP1sAfG62GPUn1O4dTHgRyE1PfqZ1czN5SVcttezO3IRik7OYWMLguD1k/gWd0l8dPsmKV+GjNk1h7+Mzqb4nYWZin9xwRB9mQgI+GXQDkauzmBCtww=="
N_gen12 = 0x9df37eb2caeb3545d134f7f4c0c5366e1271d74319c15b1954fdb3fa417238fd2d8bee657defb490dc709cea553519043ed4e2a00943dd1ca0d3f70983d0d2d83a2ea0a23978a718c8dc4d35af7ffd11ec6a6f7b44e7fcefdbae03dba75aa3081f6135692ec70bcdb3963778baf5f307e3a113e1f257fb4c587e54e144faa3861a14df1656ac16772fd510fa56a780e6e9b8672dbd9b54b6e2d7cb600af527e01a33fc9f3aaedd216c0c3f9c83d6d5f521ecb6cdc5aa826eb477d411e6501ea2a2426d8a27eef0c0eff4a41267187b15c6db254752eaa0b2913014de35f1bc7666982406404d9cf24c70e24e64f6db45d399ca78936c9b32a3f79e5cd82b8edb


# Transform the ciphers to integers
c_gen5 = int(binascii.hexlify(base64.b64decode(c_gen5)),16)
c_gen6 = int(binascii.hexlify(base64.b64decode(c_gen6)),16)
c_gen12 = int(binascii.hexlify(base64.b64decode(c_gen12)),16)

# let put the couple (c,N,3) into tuples
t_gen5 = (c_gen5,N_gen5,3)
t_gen6 = (c_gen6,N_gen6,3)
t_gen12 = (c_gen12,N_gen12,3)

# Create a liste of the previous tuple
L = [t_gen5, t_gen6, t_gen12]

# perform the broadcast attack :
plain = broadcast_attack(L)
# print the plain as ascci chars
print("This is the cracked message : " + str(binascii.unhexlify(hex(plain)[2:])))

For more details, about the attack implementation, this is a full code without any external crypto library :

'''
Created on Apr 16, 2018
@author: Nabil Diab
    
'''

from copy import copy
import binascii

class Mint:
	""" 
	Arithmetic object.
	"""
	
	def __init__(self, value : int, mod : int):
		self.value = value
		self.mod = mod
		self.refresh()

	def refresh(self):
		"""
		refresh the current value whith the modulo
		must be called whenever the value has been changed 
		"""
		self.value = self.value % self.mod

	def fast_exp(self,exp : int):
		"""	
		exponentiation of a Mint computing by the fast exponentiation algorithm
		"""
		k = copy(exp)
		pointer = 1
		p = Mint(1,self.mod)
		while (k>0):
			if(pointer & exp):
				p.value = (p.value*self.value) 
				p.refresh()
			self.value = self.value * self.value
			self.refresh()
			k = k // 2
			pointer = pointer << 1
		self.value = p.value

	def inv(self):
		"""
		self.value = self.value^-1
		"""
		self.value = euclide_algorithm(self.value, self.mod)["U"]
		self.refresh()

	def to_string(self):
		return str(self.value) + " mod " + str(self.mod)

def euclide_algorithm(a: int, b: int) -> dict :
	"""
	Extended Euclide's algorithm
	Compute the PGCD from two integers and return the Bezout's relation elements
	
	Entry : two integers A and B
	Return : a dict ( "PGCD" , "U" , "V") 
	where r is the remind and u and v are the the coefficients of the Bezout's relation
	"""
	r1 = a
	r2 = b
	u1 = 1
	u2 = 0
	v1 = 0
	v2 = 1
	
	while (r2 != 0) :
		q = r1 // r2
		rt = r1
		ut = u1
		vt = v1
		r1 = r2
		u1 = u2
		v1 = v2
		r2 = rt - q * r2
		u2 = ut - q * u2
		v2 = vt - q * v2
	
	return { "PGCD":r1 , "U":u1 , "V":v1 }

def CRT(a : Mint, b : Mint) -> Mint :
	"""
	Chiness Remainder Theorem
	Entry  : two Mint (integers modulo n)
	Return : one Mint
	"""
	r = euclide_algorithm(a.mod, b.mod)
	u = r["U"]
	v = r["V"]
	x = (a.value * v * b.mod) + (b.value * u * a.mod)
	m = Mint(x, a.mod * b.mod)
	return m

def CRT_list(L : list) -> Mint :
	"""
	Chiness Remainder Theorem
	Entry  : A list of Mint
	Return : one Mint
	"""
	length = len(L)
	while (length > 1) :
		i = 0
		while ((i*2)<length) :
			if((i*2)+1 == length) :	# case of the last element of an odd list
				L[i] = copy(L[i*2])
			else :
				L[i] = CRT(L[i*2],L[i*2+1])
			i = i+1
		length = (length >> 1) + length%2
	
	return L[0]

def find_invpow(x,n):
	"""Finds the integer component of the n'th root of x,
	an integer such that y ** n <= x < (y + 1) ** n.
	"""
	low = 1
	high = x

	while low < high:
		mid = (low + high) // 2
		if low < mid and mid**n < x:
			low = mid
		elif high > mid and mid**n > x:
			high = mid
		else:
			return mid

	return mid + 1

def broadcast_attack(L : list) -> int :
	"""
	Perform the broadcast attack from a list of message
	each message is represented as a tuple (c, N, e)
	with : * c = cipher
	       * N = modulus
	       * e = public key
	"""	

	# 1 - Verify the broadcast attack conditions
	pk = L[1][2]
	S = []
	assert  pk <= len(L), "Can't perform the broadcast attack with these conditions : too few ciphers"
	for (c,N,e) in L :
		assert pk == e, "Can't perform the broadcast attack with these conditions : the public keys are not the same"
		S.append(Mint(c,N))
	

	# 2 - CRT between the messages
	C = CRT_list(S)
	x = C.value

	m = find_invpow(x,3)

	return m


if __name__ == '__main__':
	# entrée de l'exposant
	e = 3
	# entrée des différents modules modules
	N1 = 0x985b6e5a927111aa73a8e525fe5c0b9037656a6505099af2bcbd2540245261ef3ca42885c4a2cacf49db4a3593c0cfc995fbfdd2e8d084560c6cbcdc8e0caf02ebaf3f21507561381bdabd399a5bf1247564fcd41611a089c719e63c0eb2d7a27cc80bc1146a67383e569754cea5bf3d63b81a54f548679015addd6f3a26cd58c1a25d4a24e9de59a80532a3140c41884a543961b85e31fa536f077498957a811a23eb946471b891bb0070bfc08ece10ff8fc588a846aa1c1f3a800ed407e8fc295d8c2bd1021dc7fa41696a2a3fca9c029a0a0c7b16d9928cf4a2ce3b8f73fcf3d55f04ca0c9c9164804d59d543f75d6a7514144042021b355a275e07c57deb
	N2 = 0x7de8abf2d4a082c2a947371aecdb667650938911394a40f69f827f85bd431648aee6cd282b78b4288733321b5f18d81411e4788c9c3c8156b1f1f429b481a58c7c9fdd9737162aecc84e78cf2b1788cf6c0c67b11d0b775314be3e690d20754cdb45b397f5a824cb3cdc183aea0d9642d3c0fa3114f15edadc11886eb34a54fbf4930121012148a76336ba8e3539bcd114318401c3ab0a604a0fe32ad85ab42d368bcd65bf6c67cbdaabdc1ee57c14b487162b549cdc81231cfe04e035f2c65a2de594d912221130e0f4051c121e709c97d45e78c661629b342bb8f10b3a1d4381dbc8e8e23a33decfa37fb2293f16e6d18d9dd8258c1ef19f29b41a5e640fbb
	N3 = 0x9df37eb2caeb3545d134f7f4c0c5366e1271d74319c15b1954fdb3fa417238fd2d8bee657defb490dc709cea553519043ed4e2a00943dd1ca0d3f70983d0d2d83a2ea0a23978a718c8dc4d35af7ffd11ec6a6f7b44e7fcefdbae03dba75aa3081f6135692ec70bcdb3963778baf5f307e3a113e1f257fb4c587e54e144faa3861a14df1656ac16772fd510fa56a780e6e9b8672dbd9b54b6e2d7cb600af527e01a33fc9f3aaedd216c0c3f9c83d6d5f521ecb6cdc5aa826eb477d411e6501ea2a2426d8a27eef0c0eff4a41267187b15c6db254752eaa0b2913014de35f1bc7666982406404d9cf24c70e24e64f6db45d399ca78936c9b32a3f79e5cd82b8edb
	# entrée des différents chiffrés
	cipher1 = 0x5316ee117c077c52351007e831421d180568d6ab0c33215149d64687d5f2517e5598e05dd9be192fc695b2ea8dde681c78115c0236db0bea3f7262f7b6206251359596792eeb2981683e876e9c6e907016b086bf31ab17bac430ed885f9b3bd04a6fdae3a0497ddc66d9f046da30d4e6a24dec8e965a49111217fab5c470167e962cca05b9257a22a30f4b23192b119608b8f358ff265fdbf4fe43098e7558f26f7c6b01e7001a59a1c201c104e622967cf6d4da512fdb2c8c54b24270fa299b00609220a0d0a39770fd6043257ff974456f4b737eeb27dd3019fc6de38aac5eb2c84cb656febb47f6302882a184ebadf0bf28a5f7ae775cf15f46d8f951104c
	cipher2 = 0x510e652e0859bd34b37800aa479e7eb908cd919460ddc3566fa36e58d4fa80421838f87ae4cf96c4175547a79ca73cbdd06eae00cb848264de948960436088816f05303c9bef2491bb5060db592a63af0f7db1d054b20db40bcfbc421e066fbcd0c3462e62346e75ecbc8d3192912271f488926f59dbb60b609b88df908aaa88e807013133841715a9a821555c0a88ea467fbd2deb795d06aea711a0fc0b8a77c4a66f4cff2e5c7270e81ddcfd3ed17dee7019937b62624d7c759ca0682a8a2197e97101aa324aa4b218c57b6686e8d54d02e56e3162f85f5a381a9e66ef5422e106632dcdbe84a1863eef28f1740e8a185c266d03206ff0505ef6901a980960
	cipher3 = 0x34421ed16b4e0c2eccb0dfccbe634b2491d10b2889531bbc9df1d414ecdb97ce65b1bcbde844dda04e58a5e3de3f935cdb20142c371636a834ddbdf8e41079c9f1b0c6cd509ec807b787c1bd621adda7d0399bf33dd41b5cc9b412ee75a276acdb9f98e0dc5ba77856fbec6fbed71f67004bd83026be17ea59312f0c3716b9455cc83412ca0c670b2ccac886232444b54b33d33ec963ea1a0ddf432763f520f7b3055a95d0474bf86cd3ca3f5b007c6eb618f527d4ee1d4c7811c84d4f7ea67573337949572db5eccedc846293b39858c2e0b83d64fe059dd25f1d3ec98a57e1a3364d61efe333a9be276166629fdc70441f6642023e19740391abb39810adc3

	# Mise en forme de ces données sous une liste de tuple conformément à l'attaque broadcast.
	t1 = (cipher1, N1, e)
	t2 = (cipher2, N2, e)
	t3 = (cipher3, N3, e)
	L  = [t1,t2,t3]

	print("This is the cracked message : " + str(binascii.unhexlify(hex(broadcast_attack(L))[2:])))

And the result of this code is : breizhctf

The flag is :

bzh_2k18{C0p3RSm1tH}

But I’m sorry, it is too late to save the world…