Write UP - NDH XV Wargame : Unlucky [CRYPTO]

Cet article a pour but de présenter la résolution du challenge CRYPTO unlucky présenté à la quinzième édition de la nuit du hack . Ce challenge n’a pas été résolu lors de la wargame (du moins dans le temps imparti) et était récompensé de 350 points.
Je tiens à préciser que je ne suis pas l’auteur du chall et n’ai aucune connaissance de la personne qui aurait pu l’écrire. Ce qui implique que ce chall était donc réalisable par une personne tierce.
Présentation de l'épreuve
L’épreuve se présente sous forme d’un fichier texte
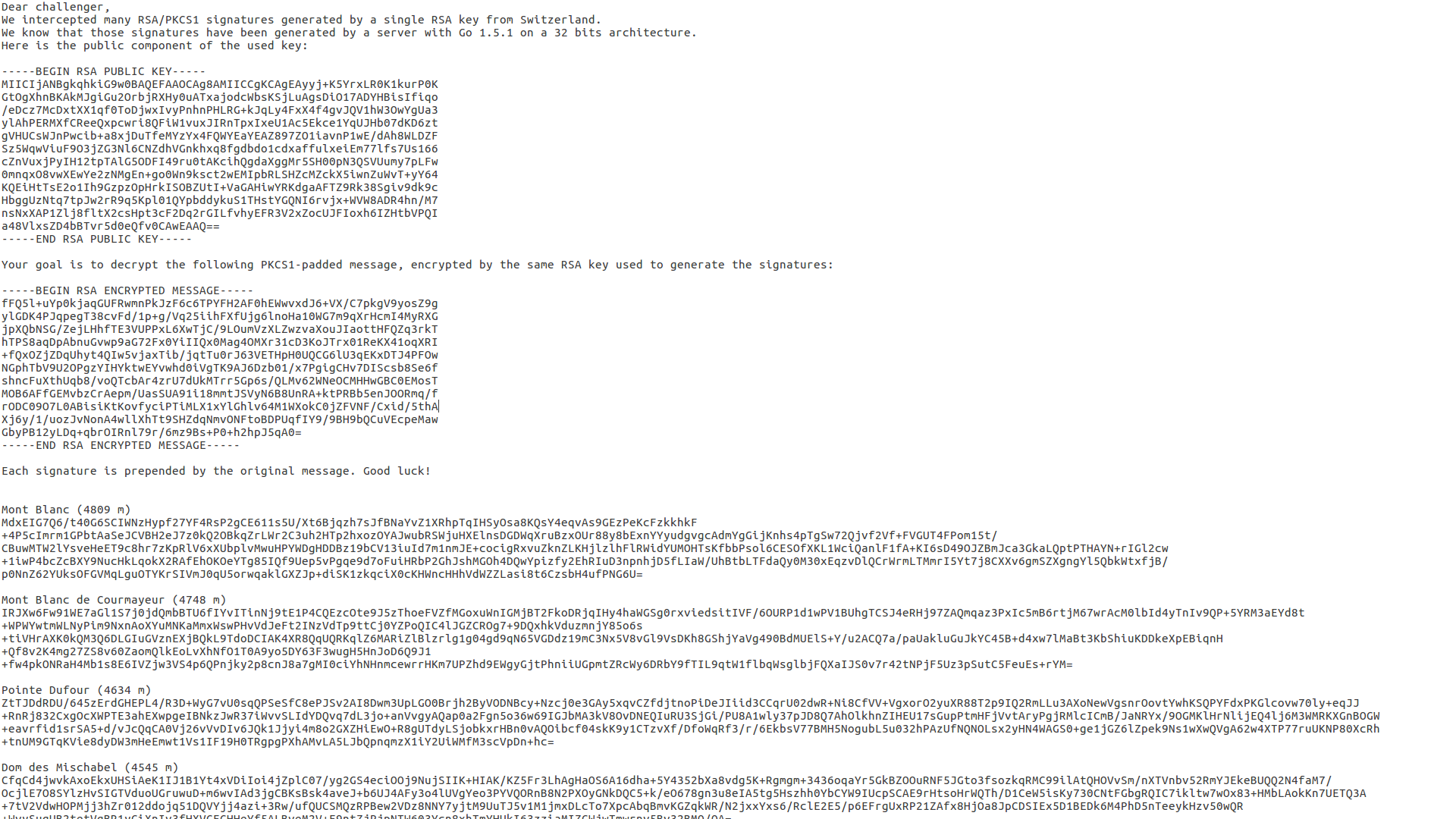
Contenant une clé publique d’un serveur 32 bits, un message chiffré avec cette clé publique (le message que nous devrons déchiffrer) ainsi que 61 signatures interceptés avec le clair correspondant.
L’algorithme de chiffrement utilisé ici est RSA avec des clés 4096 bits, ne présentant à première vue aucun signe de faiblesse.
Nous savons également que le serveur utilise le language Go 1.5.1.
CVE-2015-8618
Je remercie mon partenaire @_Bytemare de m’avoir rapidement trouvé cette CVE concernant une mise à jour de sécurité de Go v1.5.3. En effet, la vulnérabilité publiée en 2015 concerne une bibliothèque de mathématique de Go (math/big) qui est utilisée pour le chiffrement RSA. Celle-ci a la probabilité d’effectuer une erreur de calcul de 1/2^26 (1 fois sur 64 millions) sur une architecture 32 bits. Si cette erreur intervient lors d’un chiffrement RSA_CRT, cela pourrait permettre à un attaquant d’en déduire la clé privée (Détails expliqués plus bas). La CVE n’en dit pas plus quant à son exploitation, aucun POC n’est trouvable sur le net.
Cette CVE correspond parfaitement à notre scénario.
Néanmoins, afin de pouvoir exploiter une telle vulnérabilité nous allons être obligés de passer par un peu de mathématiques…
Un peu de maths
Nous allons voir dans cette partie comment avec les informations dont nous disposons, pouvons monter une attaque afin de récupérer la clé privée. Pour ceux dont ils ne s’intéressent juste à casser du chiffrement sans vouloir savoir comment cela se fait, je vous suggère de vous diriger directement vers la partie Résumé de l’exploitation.
RSA_CRT
Pour commencer, quelques rappels…
RSA
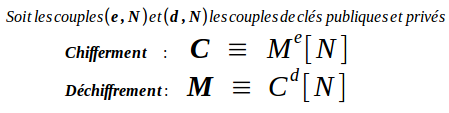
CRT - Chiness Remainder Theorem
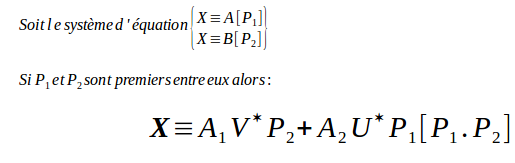
(* U et V sont issus de l’identité de bézout)
Dans RSA_CRT, le déchiffrement va donc être effectué différemment d’un RSA classique :
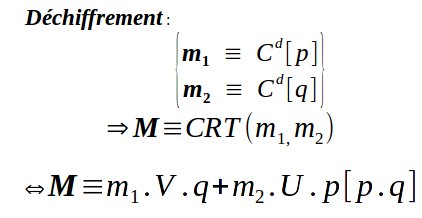
note : Ce déchiffrement est beaucoup plus faible en ressources de calcul qu’un déchiffrement classique, il est surtout utilisé sur les cartes à puce.
Que se passe-t-il si un des deux sous déchiffrement est faux ?
On va essayer sur du papier …

Ceci est l’attaque de Bellcore que nous retrouverons dans la catégorie des attaques par faute.
Résumé de l'exploitation
Ce n’est pas mal de faire des preuves sur le papier… Mais c’est mieux quand c’est appliqué ;)
Si nous récapitulons, voici notre feuille de route pour pouvoir résoudre ce challenge :
- Trouver une mauvaise signature dans la liste des signatures données
- Récupérer le message faux ainsi que le message clair sous forme d'entiers afin de pouvoir effectuer des calculs
- Calculer q = pgcd(message_faux - message, N)
- En déduire l'exposant privé d
- Construire une clé privée utilisable par une bibliothèque de cryptographie(ex : format PEM)
- Déchiffrer
I - Trouver une mauvaise signature
La première étape de notre exploitation consiste à retrouver parmi les signatures données, une qui serait mauvaise. Voici le script permettant de vérifier une signature :
#coding:utf-8
from Crypto.PublicKey import RSA
import base64
import binascii
f = open('pub.pem','r')
pk = RSA.importKey(f.read()) # pk = public key
#message = signature
message = b'MdxEIG7Q6/t40G6SCIWNzHypf27YF4RsP2gCE611s5U/Xt6Bjqzh7sJfBNaYvZ1XRhpTqIHSyOsa8KQsY4eqvAs9GEzPeKcFzkkhkF+4P5cImrm1GPbtAaSeJCVBH2eJ7z0kQ2OBkqZrLWr2C3uh2HTp2hxozOYAJwubRSWjuHXElnsDGDWqXruBzxOUr88y8bExnYYyudgvgcAdmYgGijKnhs4pTgSw72Qjvf2Vf+FVGUT4FPom15t/CBuwMTW2lYsveHeET9c8hr7zKpRlV6xXUbplvMwuHPYWDgHDDBz19bCV13iuId7m1nmJE+cocigRxvuZknZLKHjlzlhFlRWidYUMOHTsKfbbPsol6CESOfXKL1WciQanlF1fA+KI6sD49OJZBmJca3GkaLQptPTHAYN+rIGl2cw+1iwP4bcZcBXY9NucHkLqokX2RAfEhOKOeYTg85IQf9Uep5vPgqe9d7oFuiHRbP2GhJshMGOh4DQwYpizfy2EhRIuD3npnhjD5fLIaW/UhBtbLTFdaQy0M30xEqzvDlQCrWrmLTMmrI5Yt7j8CXXv6gmSZXgngYl5QbkWtxfjB/p0NnZ62YUksOFGVMqLguOTYKrSIVmJ0qU5orwqaklGXZJp+diSK1zkqciX0cKHWncHHhVdWZZLasi8t6CzsbH4ufPNG6U='
message = base64.b64decode(message) # b64 to binary
r = pk.encrypt(message,pk) # signed -> clear
print(r) # print clear message
f.close()note : le script proposé ci-dessus permet d’afficher sur le terminal la valeur du clair et la vérification se fait manuellement. Il est possible d’effectuer cette recherche de façon automatique avec un code plus élaboré.
Après avoir testé chaque signature une par une, nous trouvons enfin une signature erronée :
 En effet, au lieu de récupérer le clair “Pic Sans Nom (3913 m)”, nous nous retrouvons avec un binaire complétement incompréhensible !
En effet, au lieu de récupérer le clair “Pic Sans Nom (3913 m)”, nous nous retrouvons avec un binaire complétement incompréhensible !
Nous rappelons que la probabilité de tomber sur une telle signature avec une base de 61 signatures est exactement de 1 chance sur 524 590, ce qui explique le titre “unlucky”
II - Transformer les messages en entiers
Afin que nous puissions effectuer nos calculs mathématiques, il faut d’abord convertir deux messages (le mauvais ainsi que le clair) sous forme d’entiers.
Pour le message erroné, pas trop de problèmes, il suffit d’ajouter les lignes suivantes au code précédent :
import binascii
mfault = int(binascii.hexlify(r),16)ce qui nous permet de récupérer la valeur mFault (en hexadecimal) :

Pour le message clair, c’est un peu plus compliqué car il faut lui appliquer le padding adéquat pour que les calculs soient bons… soit PCKS1. Après une dizaine de minutes de recherches sur le net qui ne mènent à rien, j’ai décidé d’utiliser une méthode un peu maison, j’ai récupéré un message d’un même nombre de caractères que ma chaîne complété d’un padding PCKS1, et ai changé les caractères de cette chaîne par les miens… ce n’est pas une procédure habituelle… mais ça fonctionne !
Voici donc la valeur de notre message clair :

Nous avons maintenant effectuer tout les calculs que nous souhaitons avec ces messages !
III - Calcul de l'exposant privé d
Nous rappelons les étapes pour pouvoir déterminer cet exposant privé :
- Calculer q = pgcd(message_faux - message, N)
- Calculer p = N / q
- Calculer phi = (p-1) * (q - i)
- Calculer d par le biais de l'algorithme d'Euclide étendu appliqué sur e et phi
Voici le code python pour effectuer l’ensemble de ces étapes :
from Arithmetic import *
mfault = 0x60e593c7df85f6a6968ea974dcfe386780aae6cff7530fa5a8d2aac80e45ac8e433e621a7ab077e5fb57be54cce61510dc8c05029fa78fa9be1efd6c637176823502dfc8c832f17e901307ccd4b2aa07a70e1051f5eb82a382c1ff725fdc9eee0e833fdc441a882f78fe34316a7f3dcf8753ae10cf3c11fdbaec08a45d1f0207eb4cc9b42586ca72d31662ffe587a324846ced39fa3d72e01d2708f71784d0134b772063edbcd6a91b766a85d8f828328e8ea05a16c26c3776d01436588121fd79b21facd538ccb6be73f764a203a3ddee7267fa06d163f63b5a02fc99160630978381aeecd0216eb09696390c2de91fa146579383726c5e9ecef69e92ccc21e57a6627a2add000f2dcc98c11e27cb4edb0505856553f7363a781305d7145cb3824f84510a0bac51ff182d4cb75506dbc9e5cb9135f5000f04bd050adc115f867865bd34c54a7e2c29f60b13f91228e8972f8d5f34b1e88e2cd4717a1030bc8b5e69df4647031d5982f57cae6996ed69f5b2ffc65fc96307a57527d0a4d67e3047a2e717dc47e35972419ae95ffa94d5030855bbff40b29fa4e17de737b1b4dbd95ffd0c614a0bb32c1097e5899210586f100e49f55d1ead3b0003ecdc76fd4f6ae07eb7183923c075de90075c9c42cba719d74c88170fda4f04d06d601f9c5f626055313505749217d676210e6b0ed6a018e5ff19e6936f01675008a9a90906
message = 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff005069632053616e73204e6f6d202833393133206d29
N = 0xCB28FE2B962BC4B4742B592EACFD0A1AD3A05E19C128090C260886BB63AB6E34571F2D2E013C5A8E875C59BB0A4A32EE020B0388ED7B003607062B087E2AA8FDE0DCCFB31C0F1B575F5A9FD13A038F0C48BF23E78673C72D11BE909A8BCB81715F87F882F250575856DCEC188146B7CA50213C444C5DF09179E431A5CC2B8BC405896D6FBB12484674E9C48C5E53501CE4491C7B562A5091DBD3B74A0FACED8151D40AC5899CFC1C89BF9AF318C3B937DE318CD8C7815059811A604019F3DED93B589ABE73F5C04FDD021F162C36454B3E56AB0562B85F4EDE3646DCD97A08D65D8551A7921C6AF1F81D6DDA3571DC5A7DFBA5C5E8849BBEE57ECED4B35EBA7199D5BB18CFC881F5DADA530251B9383148E3DAEED2D00A72285081D69782032BE521F4D29377412554BA6CBBA4B170D269EAC4EF2FC1713061EDB334C8049FE828D169FD92C72DDB010C2296D12D21D970C65C917E62C2766E5AF4FEC98EB82901221ED4EC136A35221F46CE9CCEA47AE4212381654B48F956860078B061129D81A0054D9F51937F12822BFD764F5C1DB82053336DABBB69270DAB47DAB92A9974D506296DD77292E4B54C7B2D60640D23AAEF8F1F96556F000D1E219FF33B9EC3715C03F56658FC7E5B57D9CB07A6DDDC1760EADAB1882DFBE1C84151DD5DB1668714245228C61E88647B5B54F4086B8F15971B190F86C14EFAF97747907EFD
#compute q
q = gcd(message - mfault, N)
print("p = ",q)
#compute p
p = N // q
print("p = ",p)
#compute phi
phi = (p-1) * (q-1)
print("phi = ",phi)
#compute the private key
d = euclide_algorithm(65537, phi)["U"] % phi
print("d = ", d)J’utilise dans ce code ma propre bibliothèque cryptographique disponible sur mon github.
Nous obtenons donc comme résultat :

Nous avons donc maintenant notre exposant privé, c’est presque gagné !
IV - Construction de la clé privée
Pour cela j’utilise l’outil rsatool
python rsatool.py -n 828821012401267005051930593209588896472426297219477242130462814691925111631891312444258173488894225851927023491261837476773343905960917835489446504143517756310774928306223114111671426162481308790418796978507078145565567737809342336464198732642155751098994137993825975849016994666292054356449169824255020323180011275935389533427093009748065862422119679884569299089265204183851144870775968939924030201127448093346089172683541211474705604390471107737112885402413177952689087283914110401424448803268754588417799207317993589133196201894042967098758147607714556460581984785446709240387660990947352283396724595446096012328681845726929426798643360131595910744317120606725181337495917759892546943582110853816535122965353209789539140127862370351833546861584000320886698575749033832757971327463810681316790977928362676955163457483302232523365241898242188321893642379107638372782480021508628857042597848963995828566510618682774464978101266972685105389295927054772334931656290664686073530758014279292167425111830975163118718062325085672633019216699176085492403718885750493120165129236275529254810428072282942577035818602072562396240212443038039802451812613694072645913730526991619816700970900177099338243334311123679519911803522456716044552666877 -d 185892550182129540675623354587297971973819279839313608832807008455629754426921744993181727758567774322863044055999782551399841037485993122417250929465882898210355687186980996297167375576579836701563481648337207099221329633307284785749839894580268358109222497739769107817030086891371697010626765754409334326112318014937734268456670890493718359274039659652155028873965992283724124974526389176311752444060185231611061915395507457885876644932412756345695138662588633943063870698784709534927414635385315527032870447966296714324257304601073249818951828916273193240674650874487406795008288888809910908550108409424632883488997752586286938567354742297649824362806530577356356618794488266204587425863990135884991210112726481412637978026441437768833343469412964238376005975363914231323896708789537862905204224658022449735876053924953975814793586963995446373854676482484853280138792012242266112719262936756740801542129646412429458617841243435170915324965727970290376208937547108841525394362679468238272840382921601857009246758326934013408956042524317376855233752949181211370376156557030970795099593268453811691094904326326625238986472144367339800522747067319590768243951098790307257378800625122918326579979852342701101391901867452257648828931733 -o priv.pemqui nous génère la clé privée priv.pem suivante :

V - Déchiffrement du message
Voici le code python permettant d’effectuer cette action
#coding:utf-8
from Crypto.PublicKey import RSA
import base64
f = open('priv.pem','r')
flagenc = open('flag.enc','rb')
pk = RSA.importKey(f.read())
r = pk.decrypt(flagenc.read())
print(r)
f.close()Et nous obtenons ce résultat :

FLAG = ndh2k17_Y0d3lAyE30OoO0
Si vous avez la moindre question n’hésitez pas à me contacter sur twitter ou par mail ;)